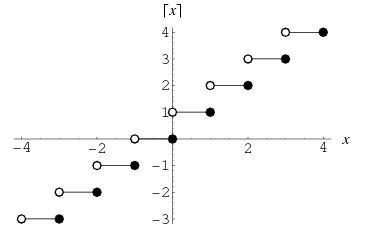
The function which gives the smallest integer , shown as the thick curve in the above plot. Schroeder
(1991) calls the ceiling function symbols the "gallows" because of the
similarity in appearance to the structure used for hangings. The name and symbol
for the ceiling function were coined by K. E. Iverson (Graham et al.
1994).
Min Max
Re
Register for Unlimited Interactive Examples >>
Im
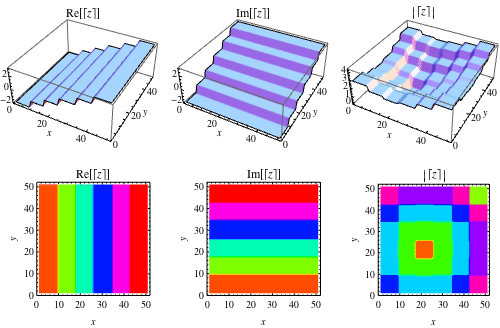
The ceiling function is implemented in Mathematica as Ceiling[z], where it is generalized to complex values of as illustrated above.
Although some authors used the symbol to denote the ceiling function (by analogy with the older notation for the floor function), this practice is strongly discouraged (Graham et al. 1994, p. 67). Also strongly discouraged is the use of the symbol to denote the ceiling function (e.g., Harary 1994, pp. 91, 93, and 118-119), since this same symbol is more commonly used to denote the fractional part of .
Since usage concerning fractional part/value and integer part/value can be confusing, the following table gives a summary of names and notations used. Here, S&O indicates Spanier and Oldham (1987).
notation name S&O Graham et al. Mathematica
ceiling function -- ceiling, least integer Ceiling[x]
congruence -- -- Mod[m, n]
floor function floor, greatest integer, integer part Floor[x]
fractional value fractional part or SawtoothWave[x]
fractional part no name FractionalPart[x]
integer part no name IntegerPart[x]
nearest integer function -- -- Round[x]
quotient -- -- Quotient[m, n]
SEE ALSO: Floor Function, Fractional Part, Integer Part, Mills' Constant, Mod, Nearest Integer Function, Power Ceilings, Quotient, Staircase Function
RELATED WOLFRAM SITES: http://functions.wolfram.com/IntegerFunctions/Ceiling/
REFERENCES:Croft, H. T.; Falconer, K. J.; and Guy, R. K. Unsolved Problems in Geometry. New York: Springer-Verlag, p. 2, 1991.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. "Integer Functions." Ch. 3 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 67-101, 1994.
Harary, F. Graph Theory. Reading, MA: Addison-Wesley, 1994.
Iverson, K. E. A Programming Language. New York: Wiley, p. 12, 1962.
Schroeder, M. Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. New York: W. H. Freeman, p. 57, 1991.
Spanier, J.; Myland, J.; and Oldham, K. B. An Atlas of Functions, 2nd ed. Washington, DC: Hemisphere, 1987.